Momentum

These kittens are playing with a Newton's cradle. When one steel ball strikes the next, the force from the first ball acts on the second ball. If the masses of the balls are the same, the second ball will move with the same velocity as the first. Here, that reaction is transferred between several balls. This is an illustration of a fundamental principle of physics called conservation of momentum.
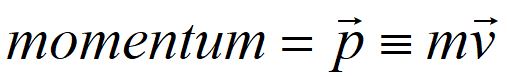
One of the conserved quantities here is the product of mass and velocity, which is called momentum.
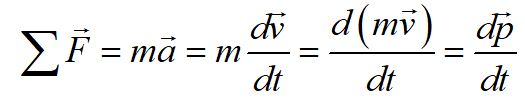
Momentum is a vector quantity, and is related to the net force as shown above. The time derivative of the momentum equals the net force. When the time derivative of momentum equals zero, the momentum is conserved.
Impulse

When a large force is exerted over a small increment of time, we call the force an impulse force.
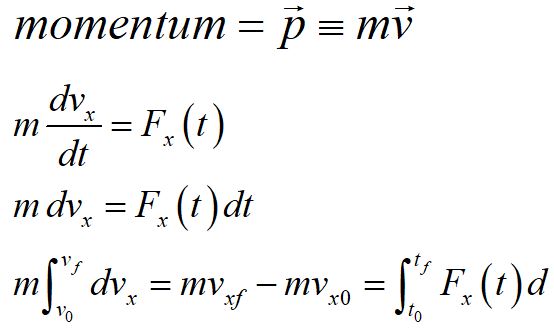
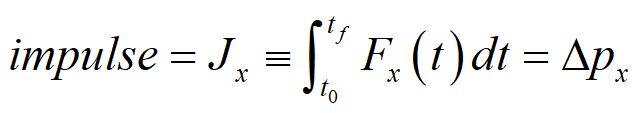
Impulse is a vector quantity, here we have defined the x-component of impulse as the area under the curve of a force over a time increment.

For example, a plot of the force as a function of time of the club on the golf ball shown above would roughly be a Gaussian function. The area under the force vs. time curve is the impulse.
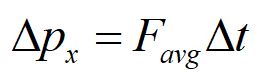
Many collisions are very complicated, and it is often useful to describe the impulse in terms of the average force. This also gives us a way to calculate the change in momentum.
Practice problems

1. A steady 3.2 N force impacts a 1.2 kg rock for 0.65 seconds. If the rock was initially moving to the right at a speed of 1.3 m/s, how fast was it moving just after the impact?
2. A 0.15 kg ball is dropped from rest from 1.25 m high and bounces back up to a height of 0.80 m. If the impact took 0.10 seconds, what was the average force exerted on the ground by the ball?
