Vectors

A vector is a mathematical construction that describes an quantity that has a direction as well as a magnitude. A scalar, by comparison, has only magnitude. Some common scalars and vectors are listed in the table below.

Distance is a scalar, and only denotes how far away an object is. Position contains information about how far away it is, as well in which direction. For example, you could say let's meet a mile from here, giving just a distance. You could give more information by saying let's meet a mile north of here. Notice that a position vector refers to an origin. Displacement is also a vector. It tells how far an object traveled and in what direction. Displacement also needs a reference point, an origin.
Speed and velocity are similarly related. Speed just tells how fast something is moving. Velocity tells how fast and in what direction something is moving.
Acceleration gives the time rate of change of velocity. We do not have a word for the scalar equivalent of acceleration, so we would typically reference the magnitude of the acceleration if we do not intend to include its direction.
Vector notation
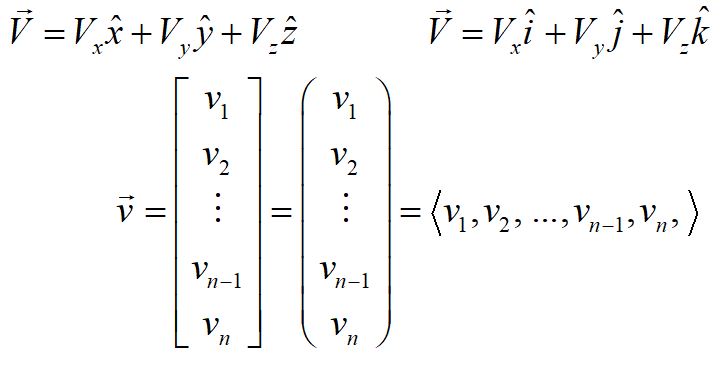
These are a few examples of vector notation. In the top two examples, the components are followed by unit vectors, denoted by a vector with a caret overhead, and read "x-hat" or "y-hat." Unit vectors have magnitude 1 by definition and point in the direction of the corresponding coordinate axis.
Sometimes the arrow over the top of the vector is left off; typically then the vector is written in bold font.
The lower examples are also vector notation, just writing the components with the unit vectors understood.
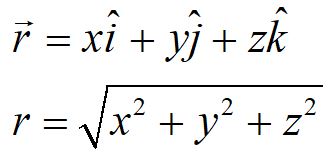
The position vector is commonly written in the form above. The magnitude of the vector can be found by taking the square root of the sum of the squares.
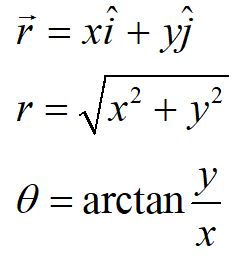
In many cases, such as typical projectile motion problems, the coordinate system can be rotated to describe the motion of the particle in a plane. This reduces a 3-D problem into a 2-D problem. The magnitude of the vector is calculated as shown above, and the angle with respect to the x-axis is found using the arctangent function. Take care to define the correct quadrant, as the first and third quadrants (and the second and fourth quadrants) give the same result, since the information regarding the sign is lost.
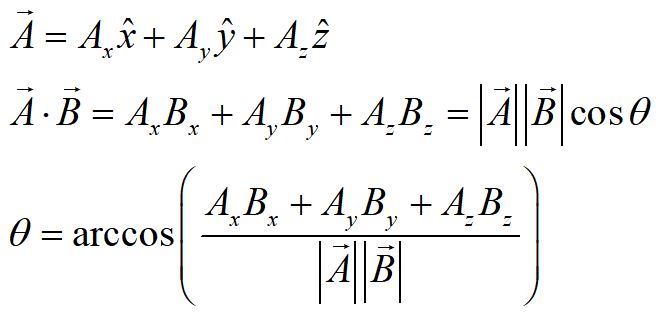
The dot product between two vectors gives the projection of one vector onto the other. It can be found by adding the products of the components of the vectors, or by multiplying the magnitudes of the vectors by the cosine of the angle between them.
Given a 3-D vector, you can find the angle it makes with respect to any of the axes using the two versions of the dot product, letting the second vector be the unit vector of the axis.
Resolving vectors into components
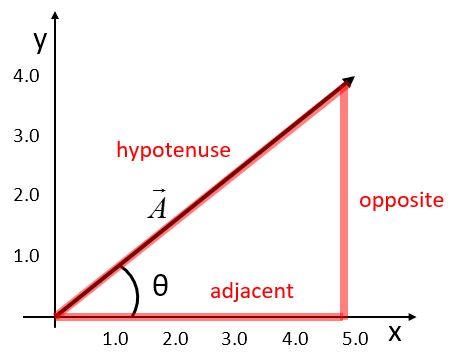
A vector is a quantity that has magnitude and direction. We represent this graphically by an arrow, where the length of the arrow represents the magnitude.
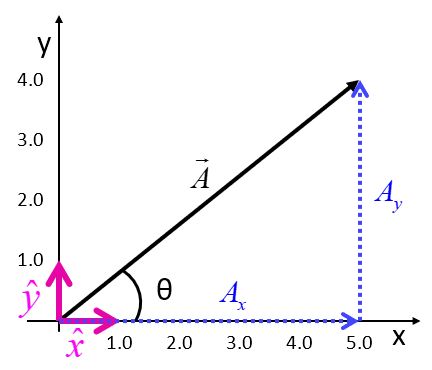
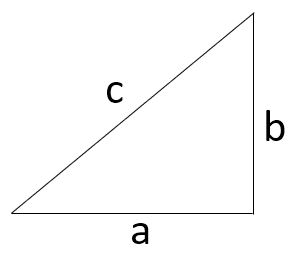
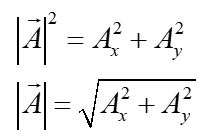
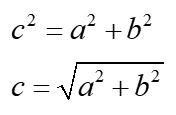
A coordinate system is a set of perpendicular lines that cross at a point called the origin, and have positive directions assigned. We can create a coordinate system to resolve our vector into components along the coordinate axes.
Here, we are really just using the Pythagorean theorem to relate the magnitude of the vector to the magnitudes of the component vectors Ax and Ay. The unit vectors x-hat and y-hat are vectors defined to have magnitude 1, pointed in the directions of the axes.
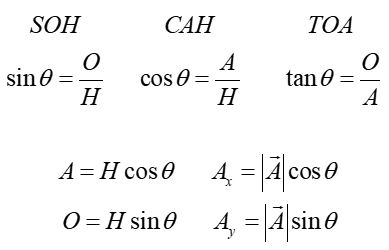
We use the trigonometric functions sine, cosine and tangent to relate the magnitude of the vector to its components.
A vector can be resolved into components by taking the cosine of the angle to find the x-component and taking the sine to find the y-component, as long as the angle is defined with respect to the x-axis. If the angle is defined with respect to the y-axis, the sine and cosine functions are switched.
Adding vectors
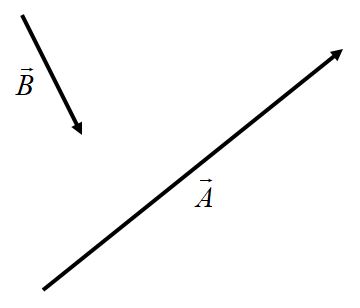
Addition between two or more vectors can be done graphically. In flat space, without any loss of generalization, a vector can be moved anywhere on a coordinate system, as long as its magnitude and direction are not changed.
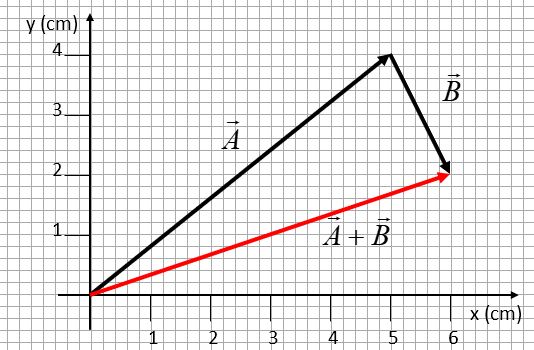
The vectors can be added by placing the tail of the first vector to the origin, and then placing the tail of the second vector at the tip of the first. The resultant vector is found by placing its tail at the origin and its tip at the tip of the second vector.
What is the magnitude and direction of the resultant vector?
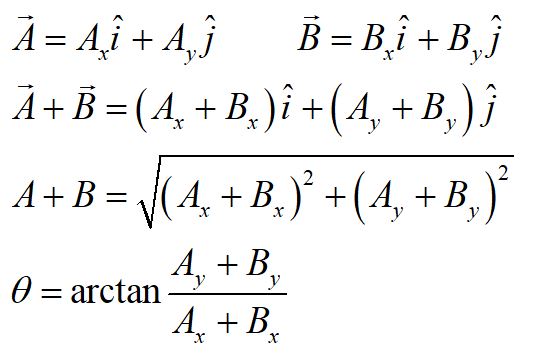
Adding two vectors can be done by breaking the vectors into components, and adding the components separately. The magnitude and direction of the resultant vector can be found as shown above. This method can be extrapolated to add three or more vectors.
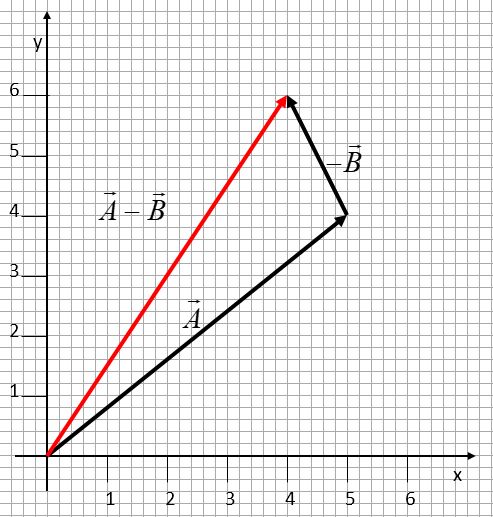
A vector can be subtracted from another by adding the negative of the vector to be subtracted.
