Conservation of momentum

For a system of interacting particles, the sum of all the interaction forces internal to the system is zero. The net force on the system is the time rate of change of the momentum of the system.

For the total momentum P:

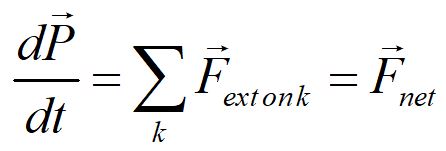
If objects collide in the absence of external forces, momentum is conserved for the system. This means that the final momentum of the system equals the initial momentum of the system.

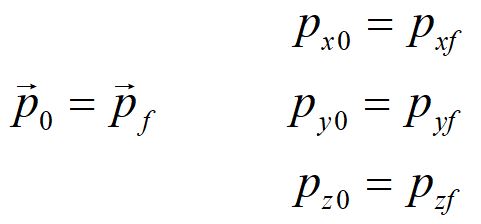
Note that this is a vector equation. Momentum is conserved in each vector component. If we work in one component at a time, we can treat each equation as a scalar equation.

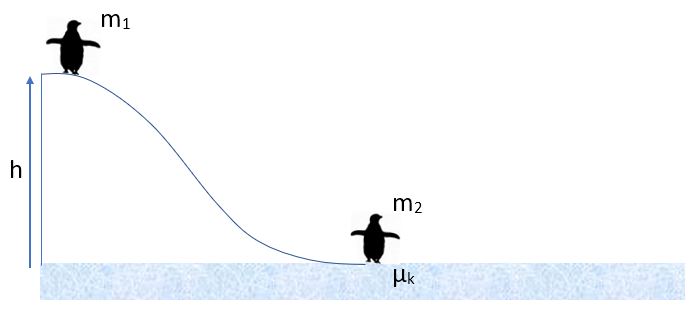
Let's consider a one-dimensional collision between two massive objects.

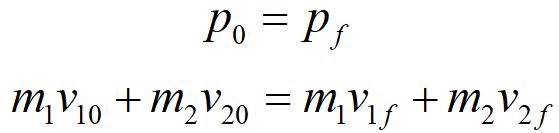
Note that momentum is not conserved for each massive object, but for the system as a whole. We need to consider all of the massive particles involved and their velocities.

Elastic and inelastic collisions

Elastic collisions occur when two objects bounce perfectly off of each other without losing any energy in the collision. In an elastic collision, kinetic energy is conserved as well as momentum.

Completely inelastic collisions occur when two objects collide and stick together. Kinetic energy is lost in an inelastic collision but momentum is conserved.

Most collisions are neither perfectly elastic or completely inelastic. However, we can learn a great deal about collisions by considering these extreme cases.

It should also be noted that an explosion, where one object is blown apart into two or more pieces, can be modeled as a completely inelastic collision happening in reverse.

Conservation of kinetic energy

When two objects collide completely elastically, energy is conserved. For a simple case where both objects are on level ground, kinetic energy is conserved.

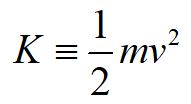
The kinetic energy of a massive object is defined as one half its mass times its velocity squared. The velocity squared is really a dot product. Notice that kinetic energy is a scalar quantity.

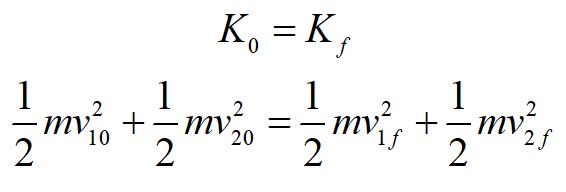
When kinetic energy of a system of particles is conserved, the total initial kinetic energy equals the total final kinetic energy.

For an inelastic collision, where the objects stick together, the conservation equation for kinetic energy will not be satisfied. The difference between the final kinetic energy of the particles in the system and the initial kinetic energy equals the energy lost during the collision. This energy typically goes into friction and other complications such as deformation.

This website from The Physics Classroom contains an interactive simulation of two carts undergoing elastic and inelastic collisions.

Practice problems

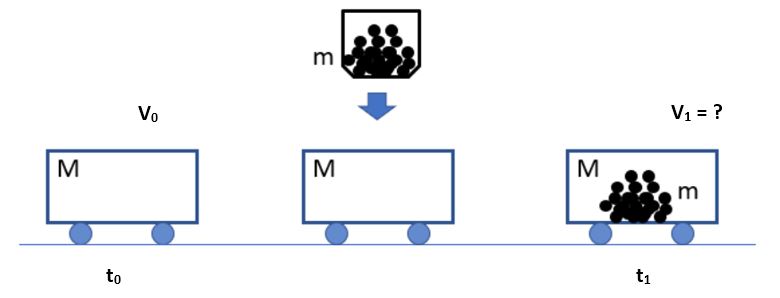
1. A. A train car of mass M is moving at an initial velocity v0. The car moves under a chute, which dumps coal of mass m into the car. What is the final velocity of the car + coal?

Consider the case where v0 = 2.2 m/s and M = 5m.

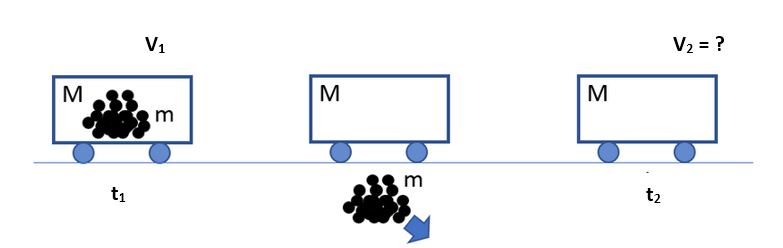
     B. The train car carrying the coal now rolls over a pit, drops the coal, and rolls on. What is the final velocity of the empty train car?

3. A 3600 kg cannon is on frictionless level ground. It fires a 28 kg cannonball with a muzzle velocity of 750 m/s.

  A. What is the velocity of the cannon just after the cannonball is fired?

  B. How much energy is expended in firing the cannonball?

4. A rocket carrying a satellite moves with initial velocity v0 in the positive
x-direction. The total mass of the rocket and satellite is m, and the rocket is twice as massive as the satellite.

The rocket launches the satellite such that the satellite moves in the positive y-direction at a speed of 2v0.

Find the final velocity of the rocket, in terms of v0.

5. A 12 g bullet is fired into a 1.5 kg pendulum hanging initially at rest from a 1.4 m string. The bullet is embedded in the pendulum bob, raising it to a maximum angle of 35 degrees. What is the initial speed of the bullet?