Relative motion
Relative motion is when two or more objects move with respect to each other. We have already done some problems involving relative motion in one dimension. Here, we will look at another way to represent that motion and also work on systems where relative motion can be described in the framework of two dimensional kinematics.

1-D relative velocity
We can describe relative velocities in one dimension when objects are moving in parallel paths.
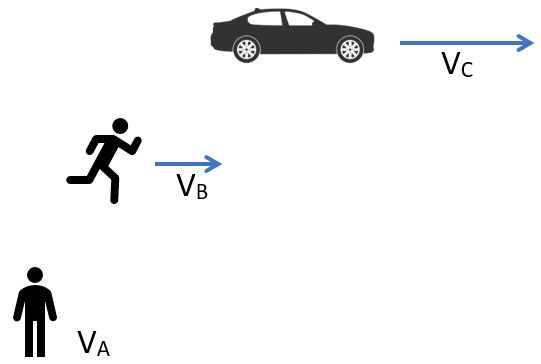
To Andy, a stationary observer in the Earth's reference frame, Bob is running in the positive x direction with speed VB while Chevy is moving in the positive x direction with speed Vc.
What does Chevy see? To him, it looks like the runner Bob is moving backward and Andy is moving backward even faster.
Neither of these observations is more "correct" than the other, they are simply different taken from different frames of reference.
To make this more clear, we can specify a velocity in terms of a reference frame.
(Vx)CA is defined as Chevy's velocity with respect to Andy. In other words, it is how Andy would measure Chevy's velocity. (Vx)AC is Andy's velocity as seen by Chevy.
(Vx)AC = -(Vx)CA
The velocity is equal and opposite to the two viewers.
Adding relative velocities
It makes sense that the speed of the car that Andy sees is the speed of the car that Bob sees plus the speed of Bob that Andy sees.
(Vx)CA = (Vx)CB + (Vx)BA
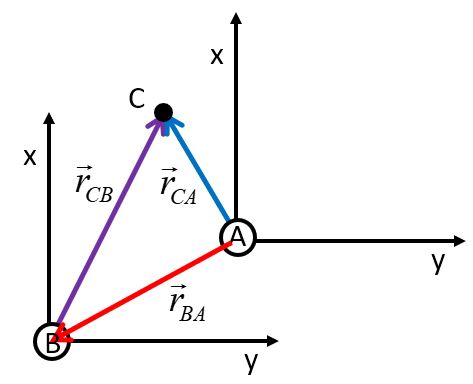
We can diagram the point C as seen by the reference frames A and B.
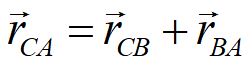
We can write the vector addition in vector notation.
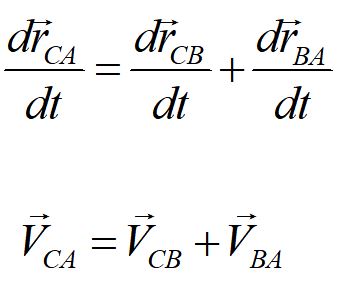
Taking the time derivative of our position vector equation allows us to write an equation for the addition of velocity vectors. When adding velocity vectors to find relative velocities, be careful to add the vectors by components.
Practice problems
1. A boat takes 3.0 hours to travel 30 miles downstream, then 5.0 hours to return. How fast is the river flowing?
2. Two cars approach an intersection, at constant speeds. Car A is traveling North at 2.5 m/s, while Car B is traveling East at 4.5 m/s. Find the relative velocity of Car A as seen by Car B, VAB.
3. A boat has a motor that pushes it through still water at a speed of 3.0 m/s. The pilot wishes to cross a river that has a current of 2.0 m/s. At what angle must she steer the boat (from the perpendicular to the bank) such that the boat will go straight across?
