Problem-solving example
We will apply our fundamental knowledge of circular motion to solve a problem using the Required Solution Format.

A ball of mass m on the end of a string of length L is swung in a vertical circle.
a. Find the minimum speed possible at the top of the circle.
b. Find the tension in the string at the bottom of the circle, assuming that the speed is twice that at the top.
Required solution format
1. Understand the problem and devise a plan
a. Translate the problem
A ball is moving vertically in nonuniform circular motion. For part a, we will find the minimum possible speed at the top. For part b, we will find the tension at the bottom, given that the speed at the bottom is twice that at the top.
What is given and what will be determined? Translate the problem statement into math, using the form "symbol equals number units."
We were not given specific values here, so we will list our known variables and our variable to be determined.
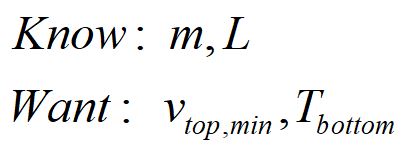
b. Determine applicable concepts and/or laws and assumptions and/or simplifications
Applicable concepts
- Nonuniform circular motion
- Newton's second law
Assumptions
What assumptions have we made?
- The string remains taut
- The string is massless, inelastic
- The ball is treated as a particle
- The gravitational force is constant
This step helps you to devise a strategy for your solution. Our ball is being swung in a circle, so circular motion is a good approach to use. It is moving at different speeds at different times, so we will use nonuniform circular motion.
The tension in the string is what keeps the ball moving in a circle, so a force approach will be helpful. We also know the velocity will be perpendicular to the tension force at all times.
In the context of problem-solving in physics, an assumption is a simplification of the physical system that makes the problem easier to solve. It typically entails disregarding an aspect of the system that is small compared to other aspects. Can you think of other assumptions that would be appropriate for this problem?
2. Represent the problem physically and mathematically
a. Represent physically: Draw an appropriate type of physical representation such as a diagram and/or graph
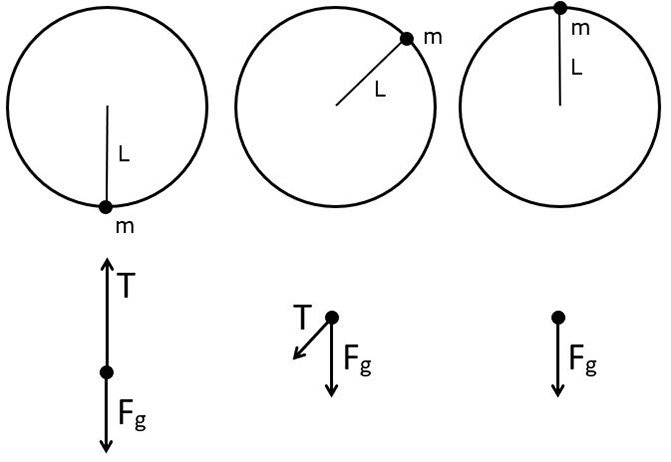
We have represented our system at different parts of the swing, with a simple conceptual diagram coupled with a free-body diagram at each position.
In general, different kinds of problems may require different kinds of representations.
b. Represent the concepts and/or laws mathematically
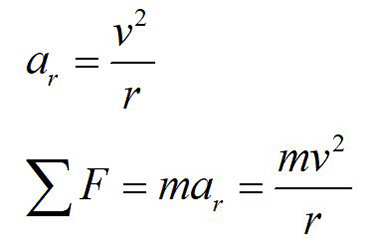
These are the main equations we will be using. Note that the radial acceleration equation holds true, even for nonuniform circular motion. In this case, it relates the speed to the radial acceleration at any point in time.
3. Solve for unknown quantities

Here we write the equations specifically for the system at hand. We use the subscript T to denote the top of the swing.
Note that the tension term is positive. By convention, we define the direction toward the center of the circle as positive.
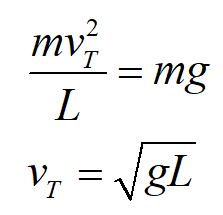
We symbolically solve for the desired variable, making sure that our answer is in terms of given variables.
Note that we dropped the TT term. For the minimum speed at the very top, the tension in the string would go to zero.
Even if we were given numerical values for our variables, we would perform a symbolic solution before converting to numbers to find the answer.

Now we follow a similar procedure for part b, when the ball is at the bottom of the swing. We rewrite the basic equations using the subscript B to denote the position at the bottom. We again define the direction toward the center of the circle as positive.

We were given the information that the speed at the bottom of the swing is twice the speed at the top, so we use our answer from part a to define the speed. We then symbolically solve the equation for our desired variable, making sure our answer is in terms of given variables.
4. Is the answer reasonable? Does it make physical sense?
Now we need to check our answer to see if it makes sense. There are three main ways to do this:
- Units
- Order of magnitude
- Limiting cases
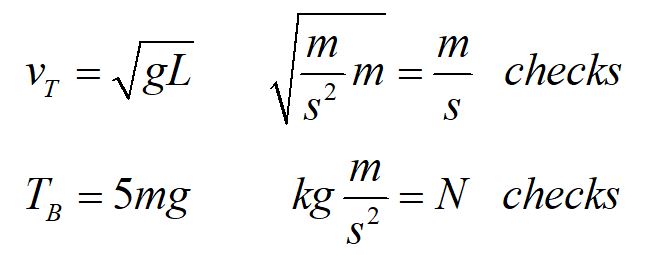
Our units check out ok. This does not necessarily mean our answer is correct, but if our units did not check out, it would mean that our answer was wrong.
Since we do not have actual values, we cannot do an order of magnitude check on the numerical answers. If we did have values, we would consider whether or not the numerical answer was within a believable range. We can check the answer to part b. It seems believable that the acceleration of the mass could be 4 g's. It should not be less than g. If the answer was tens or hundreds of g's, we should start to worry about the order of magnitude.
Considering limiting cases means analyzing the answer in terms of the placement of the variables.
For the speed at the top, you should check to make sure that the placement of g and L make sense for the speed.
In this case, the larger g is, the larger the speed. This makes sense, since gravity is accelerating downward and the ball would have to go faster to keep the string taut even at the top. If there was no gravity and g went to zero, the speed would also go to zero, since there would be no need to keep the ball moving.
The larger L is, the larger the speed. For larger L, there is a bigger change in potential energy from the bottom of the circle to the top. The higher the ball is swung, the faster it must be moving. If L goes to zero, the ball would not be moving at all, so it makes sense that decreasing L would agree with decreasing v.
For part b, it makes sense that a larger mass would have a larger tension at the bottom, since a larger mass would be harder to lift. As mass goes to zero, the tension also goes to zero, by the same logic. It also makes sense that stronger gravitational acceleration would give larger tension. The tension would be larger in this case even if the ball were not swinging. Also, if the gravitational acceleration was smaller, it would make sense that the tension would decrease.
