Damped oscillations
Damping can occur in oscillating systems due to air resistance, internal friction, etc. The sources of damping are typically lumped together under the name "damping forces" and mathematically included as a linear term in the force equation. For example, the drag force -bv is included in the equation of motion of a mass on a spring:
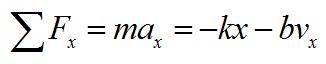
We can write this as a differential equation, and confirm the solution:
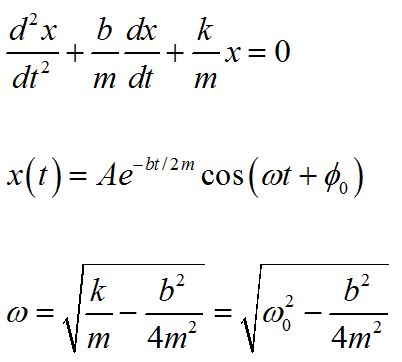
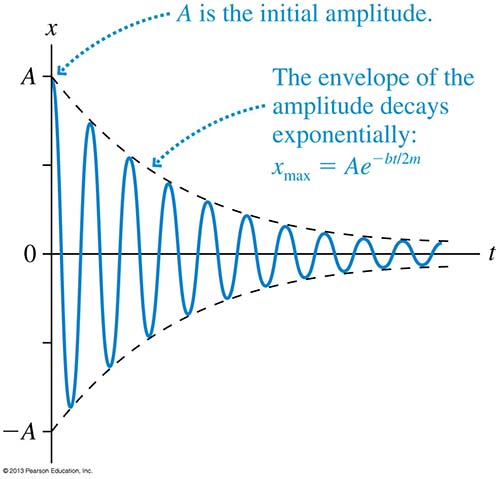
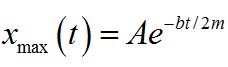

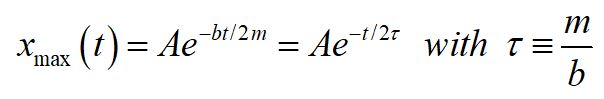
We can write the damped amplitude as a function of time for a lightly damped oscillator. A here is the initial amplitude.
Practice problem: A ball of mass m is oscillating on a spring with a period T. The amplitude decreases by 3.0% during each oscillation. If the initial amplitude is 0.25 m, what will be the amplitude after 30 oscillations? Consider the case for m = 0.65 kg, T = 0.88s.
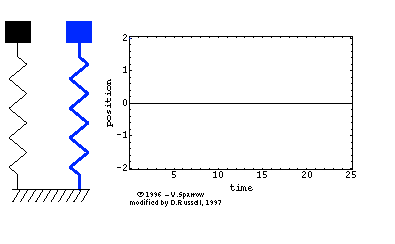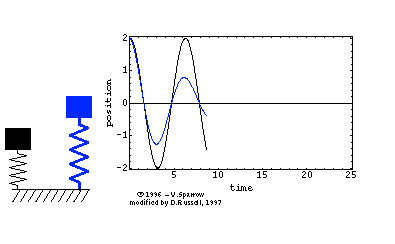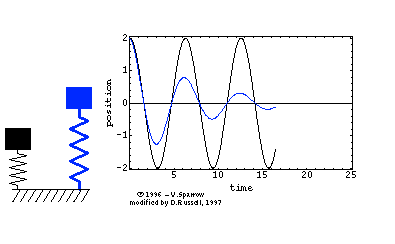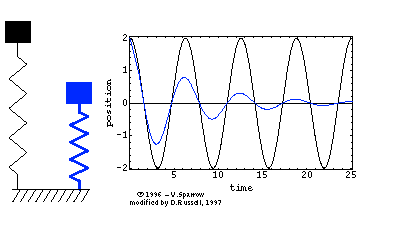
Driven oscillators and resonance

When some mechanism provides an external periodic force to an oscillator, the oscillator is said to be driven. For example, if you push a child on a swing periodically, timing the pushes to help the child swing higher, you are driving the oscillation.
If you stop driving the oscillation and just let the child keep swinging, she will swing at the natural frequency f0 for the system. The frequency at which you push the child is called the driving frequency fext. The driving frequency is independent of the natural frequency.
When you do push the child at the same frequency as the natural frequency, she goes higher and higher. This is an example of resonance. the condition of resonance is when the driving frequency equals the natural frequency.
fext = f0 resonance condition
Because of this relationship between the driving frequency and the natural frequency, the natural frequency is often called the resonance frequency.
Animation courtesy of Dr. Dan Russell, Grad. Prog. Acoustics, Penn State