Simple Harmonic Oscillator energy

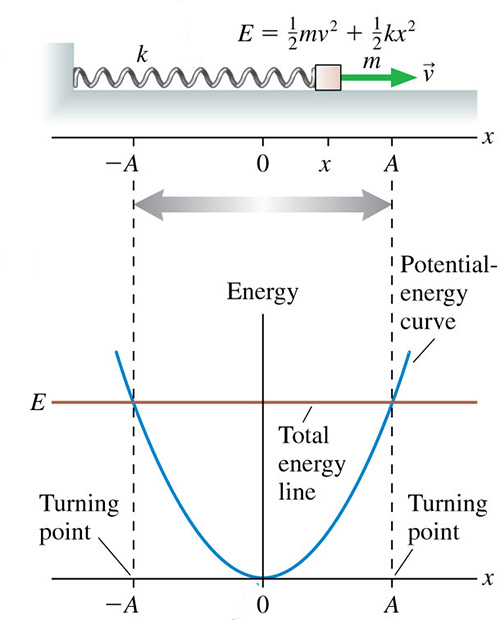
Kinetic energy is denoted as the height between the potential energy and the total energy in an energy diagram. The turning points, where the potential energy equals the total energy, have zero kinetic energy. Where the system goes to zero potential energy, the mass moves at maximum velocity, since all of the energy is kinetic energy.

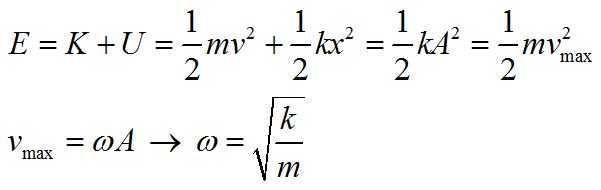
Using conservation of energy, and our previous definition of vmax, we can find an expression for the frequency of oscillation. Note that frequency does not depend on the amplitude and that energy goes as the square of the amplitude.

The Pendulum

• Restoring force
• Period

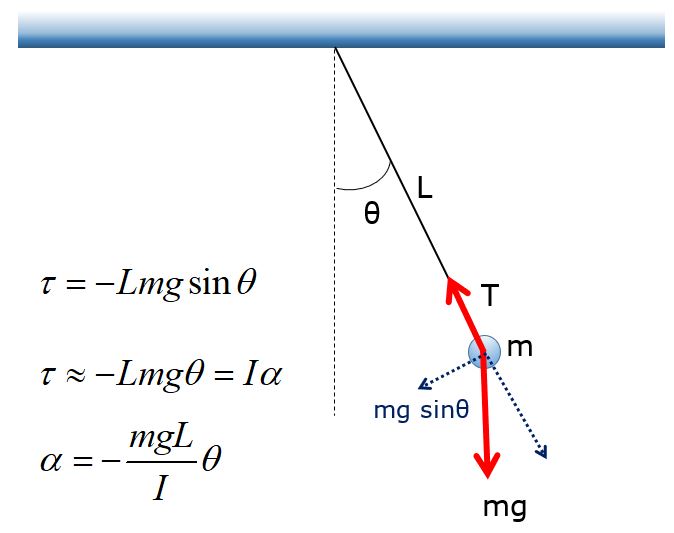
We can derive the period of a physical pendulum by examining the torque caused by the restoring force. Here, the torque is negative because it causes a clockwise motion for positive theta and a counterclockwise motion for negative theta.

This is the angular equivalent of the linear the SHO equation of motion:

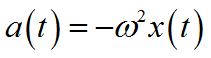
Comparing these two equations, we find:

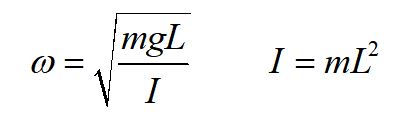
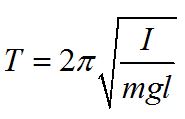
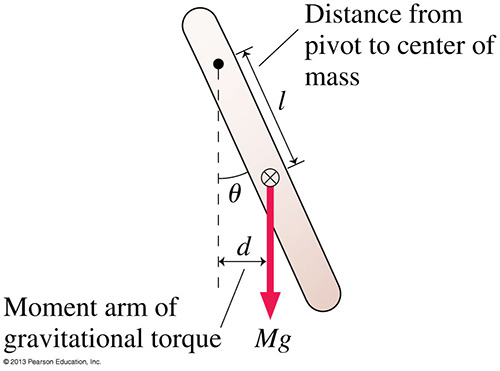
For a physical pendulum, we use the general form for the period. Note that l is the distance from the pivot to the center of mass and m refers to the total mass.

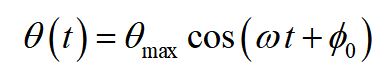
We use a change of variable from the simple harmonic oscillator equation to write the equation of motion for a pendulum in terms of the phase angle and maximum angle, instead of the displacement and maximum displacement.

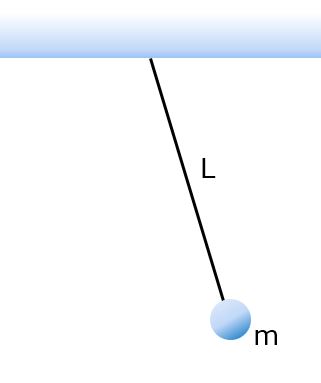
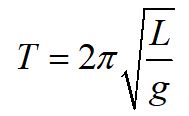
For a simple pendulum, we can let the mass of the string go to zero and the moment of inertia takes a simple form. Substituting these values into our equation for a physical pendulum, the period for a simple pendulum reduces to the form shown above. The period of a simple pendulum only depends on the length of the string and the force due to gravity, in the limit of the small angle approximation.

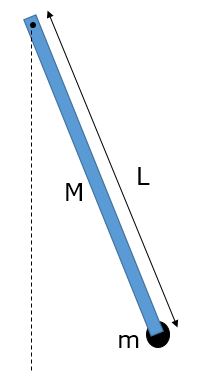
Practice problem: find the period of a physical pendulum consisting of a rod with mass M and length L, with mass m attached as shown, pivoting about the end of the rod.