Phase difference
- The phase constant tells what the wave is doing at t = 0, x = 0
- The phase difference: difference between the phases of two waves

These two waves are completely out of phase. Where one has a crest, the other has a trough, so they exhibit completely destructive interference.









A. Move speaker 1 forward 1.0 m
B. Move speaker 1 forward 0.5 m
C. Move speaker 1 backward 0.5 m
D. Move speaker 1 backward 1.0 m
E. Don't move anything, they already have completely constructive interference
2. Assume the blue circles in the diagram represent wave crests. Which points are positions of complete constructive interference?

Use this interactive PhET simulation to explore superposition, and find locations of completely constructive interference and completely destructive interference for waves emanating from two sources.
Practice problems
1. Two completely out-of-phase radio antennas at x = +300 m and -300 m are emitting 3.0 MHz waves. Is the point (x, y) = (300 m, 800 m) a point of completely constructive interference, completely destructive interference, or neither?



Amplitude function

The amplitude function is useful for the special case where the two sources have the same amplitude, and their displacement from each other is known, as well as their initial phase difference.

The black dots in the images above represent two sources of sound waves
- in phase (left)
- out of phase (right)
The colors indicate the amplitude of the superposed sound.
The pale green lines show where destructive interference occurs in space.
Thin-film optical coatings
When light strikes a surface from a lower index of refraction to a higher index of refraction, the light wave undergoes a phase shift of pi radians.
When light comes from a higher index of refraction to a lower index of refraction, there is no phase shift.
You can think of this in terms of the wave on a string encountering a hard or soft boundary. Reflecting from the hard boundary causes a phase shift, where reflecting from the soft boundary does not.
In thin-film coatings, the phase-shifted, light reflected from the outer boundary interferes with the light reflected from the inner boundary.
If the interfering waves are in phase, they produce a "strong reflection" because they undergo constructive interference. However, the thickness of the film can be adjusted such that the waves undergo destructive interference, by ensuring that the waves are out of phase when they interfere. Thin-film coatings can be used to create anti-reflective coatings for optical lenses.
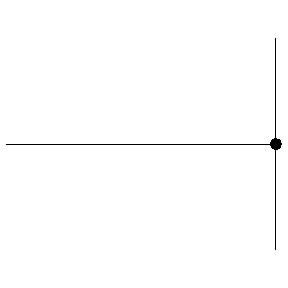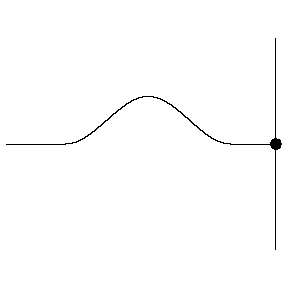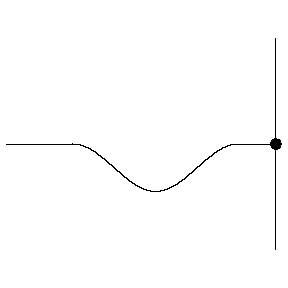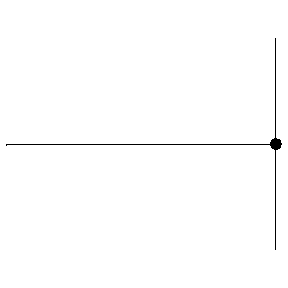
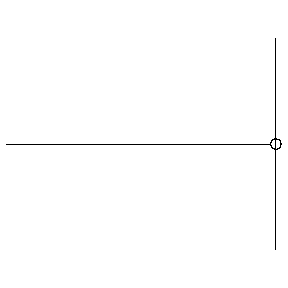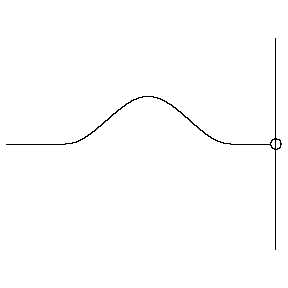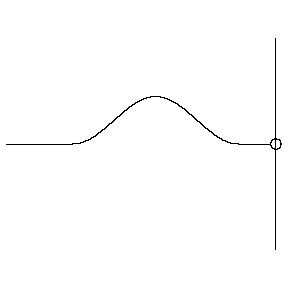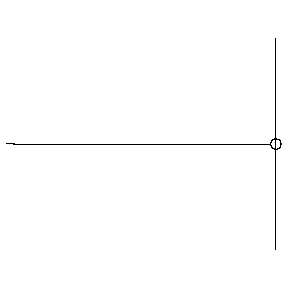
Animations courtesy of Dr. Dan Russell, Grad. Prog. Acoustics, Penn State