Wave reflections
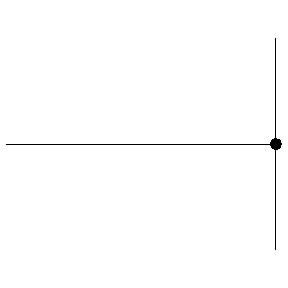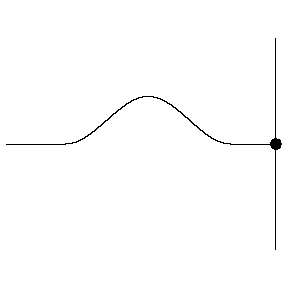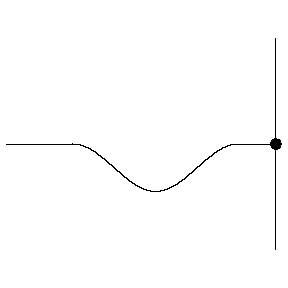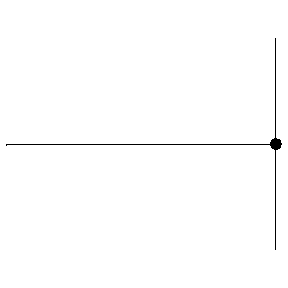
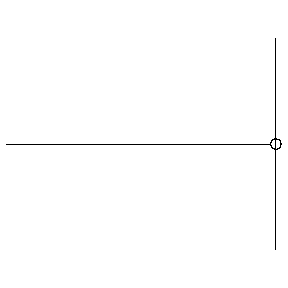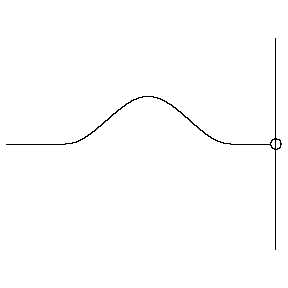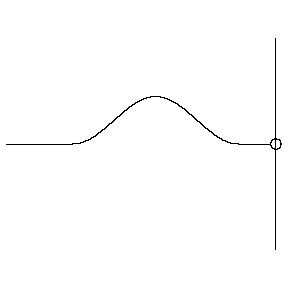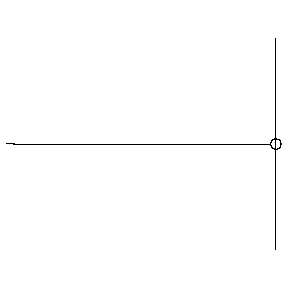
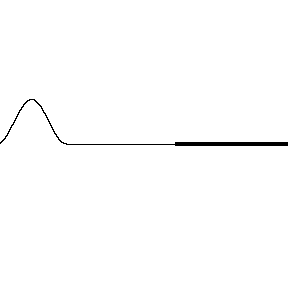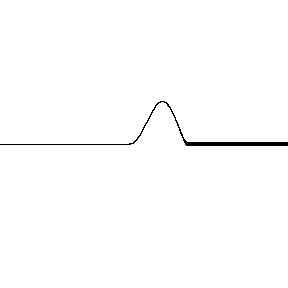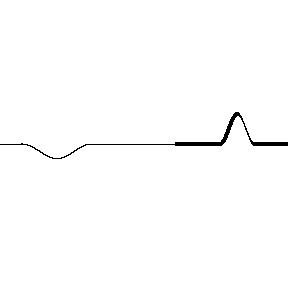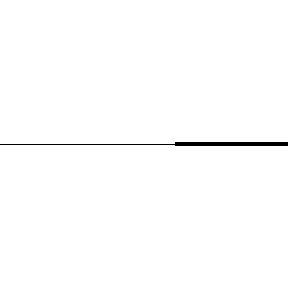
Reflections can occur when a wave encounters a boundary. A wave on a string can encounter hard and soft boundaries, with different results:
- Hard boundary: reflected wave changes its polarity
- Soft boundary: Reflected wave keeps its polarity

© 2013 Pearson Education, Inc
When a wave encounters a discontinuity, there can be reflection and transmission at the boundary.
A change in density of the string acts like a boundary
-
Low to high density is like a hard boundary
- Polarity shift upon reflection
- Reflected wave: amplitude is lower, wavelength is the same
- Transmitted wave: amplitude is lower, wavelength is narrower
-
High to low density is like a soft boundary
- No shift in polarity
- Transmitted wave: amplitude is higher, wavelength is wider
- Reflected wave: amplitude is lower, wavelength is the same
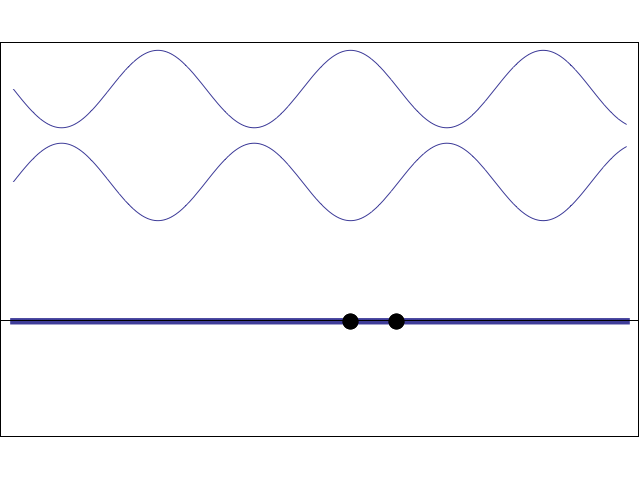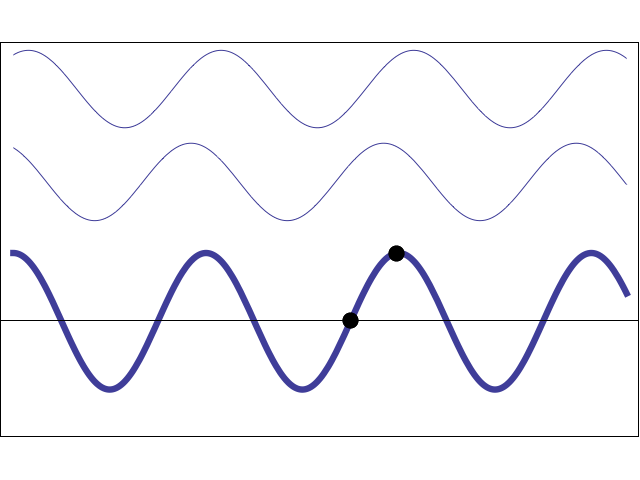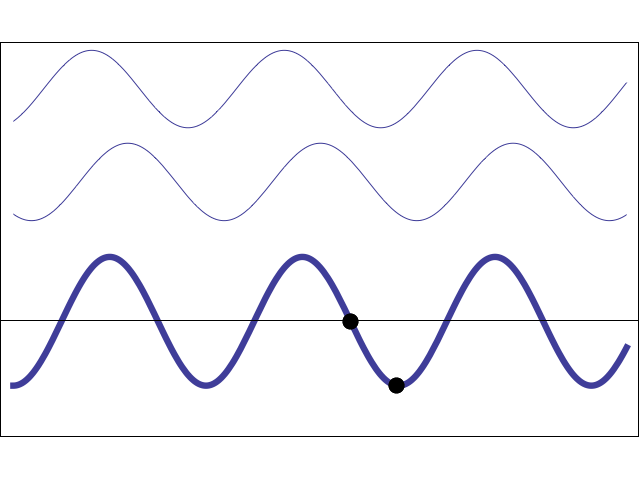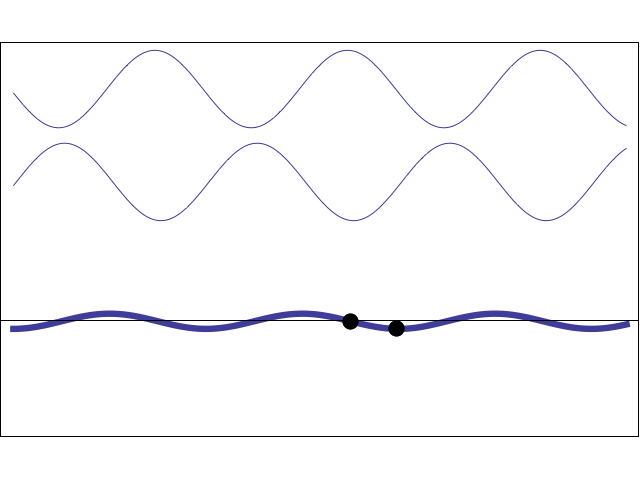
Standing waves
Standing waves are produced when two waves of identical frequency, traveling in opposite directions, interfere with each other.
Fixed points that undergo zero net displacement are called nodes.
Halfway between the nodes, points that undergo maximum oscillation are called antinodes.


© 2013 Pearson Education, Inc
Harmonics
Standing waves with the lowest energy are called fundamentals. For a standing wave on a string with fixed ends, the wave has a node at each end and one antinode in the center. This makes up half of the wavelength, so the wavelength is twice the length of the string.
The next wave is called the second harmonic (has two antinodes). The spectrum of harmonics for a wave on a string all have nodes at each end, with an increasing number of nodes in-between.
fundamental
(1st harmonic)
2nd harmonic
3rd harmonic
4th harmonic


The position of the position of the mth node is a function of the wavelength.
- m is the number of antinodes
- f1 is called the fundamental frequency of a standing wave
Standing waves can also exist in pipes supporting longitudinal sound waves. There are three main cases, where the two ends are both closed, both open, or have one end open and one end closed.



© 2013 Pearson Education, Inc

- Closed end of a pipe supports a node
- Open end of a pipe supports an antinode
- Higher frequency waves are called harmonics
- f2 = second harmonic
- f3 = 3rd harmonic, etc

Practice problems
1. A 0.85 m long wire has a mass of 0.0022 kg and a tension of 52 N. What is its fundamental frequency?
2. An open-open pipe is 1.6 m long. What is its second harmonic frequency?
3. An open-closed pipe is 0.85 m long. What is its third harmonic frequency?
4. The wire in the image below has a mass of 0.0035 kg. What is the frequency of the third harmonic?

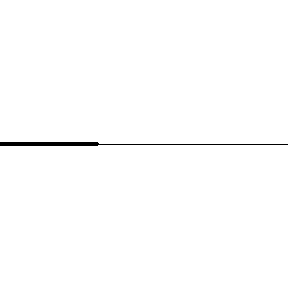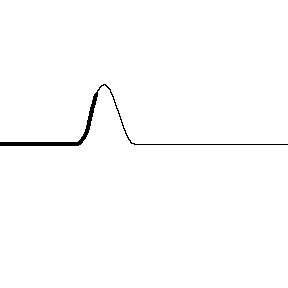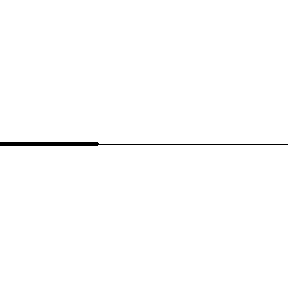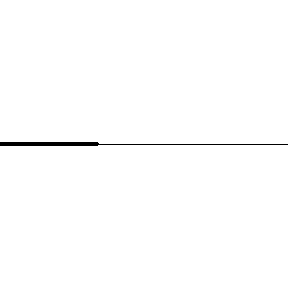
Animations courtesy of Dr. Dan Russell, Grad. Prog. Acoustics, Penn State