Doppler shift

The Doppler shift is an effective change in frequency or wavelength detected when the observer or source, or both, are in motion relative to each other.
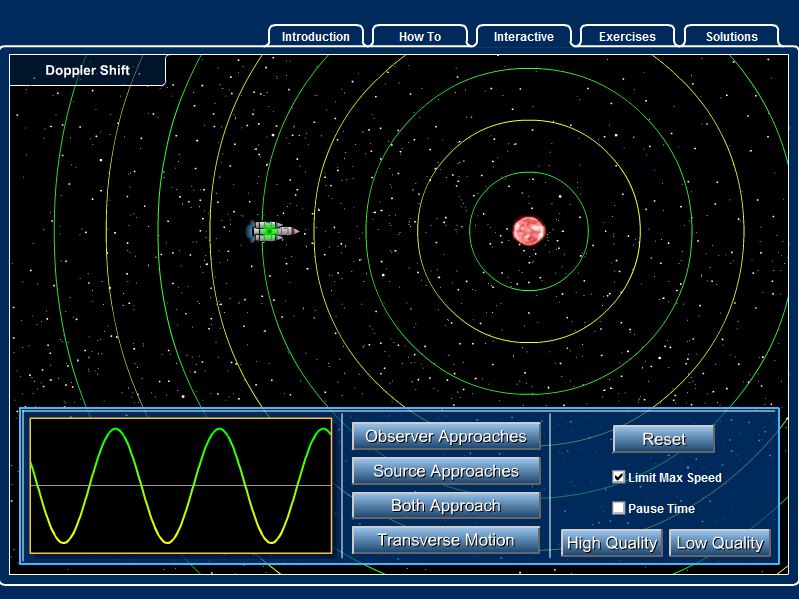
The Doppler shift arises when there is relative motion between a wave source and an observer. If the distance between the two is decreasing, the observed frequency of the wave is higher than the frequency that would be heard if the source and observer were at rest with respect to each other. If the distance between the two is increasing, the observed frequency is lower.
Moving observer, stationary source

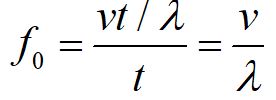
We will call this frequency f0 since the source and observer are not moving with respect to each other.
Now consider the case where the observer is moving toward the source.
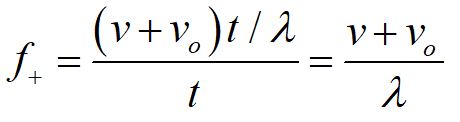
Now the waves seem to be coming faster in the frame of the observer. The observed frequency is higher, denoted by the f+. The speed of the observer is denoted by vo.
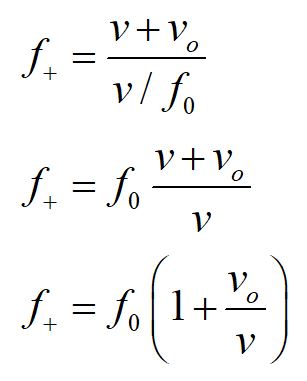
A little algebra allows us to write the Doppler shift equation in a simpler form, in terms of the rest frame frequency.
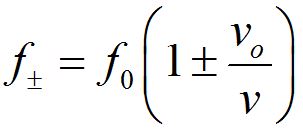
We can derive the frequency detected by the observer when the observer is moving away from the source in an identical fashion. The formula above is a compact form we can use for both cases.
Note that f+ denotes a higher frequency, corresponding to the observer moving toward the source, while f- denotes a lower frequency, corresponding to the observer moving away from the source.
These formulas can be rewritten in terms of wavelength, using the relationship between velocity, wavelength and frequency.
Moving source, stationary observer
When the source of the sound is moving, it changes the wavelength of the sound. This subtle distinction means the formula for a moving source is fundamentally different from that of a moving observer.
Consider the case where the source is moving toward the observer.
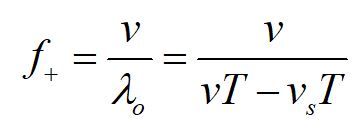

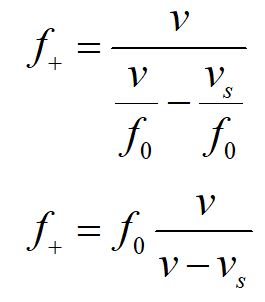
A little algebra allows us to rewrite our formula in terms of the rest frame frequency.
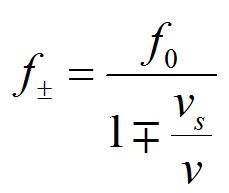
An identical method allows us to derive the frequency from a moving source detected by a stationary observer, and we can combine the two equations into one equation as seen above.
Note that f+ denotes a higher frequency, corresponding to the source moving toward the observer, while f- denotes a lower frequency, corresponding to the source moving away from the observer.
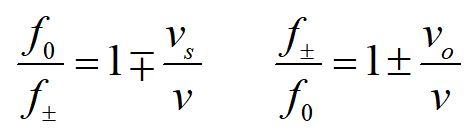
The Doppler shift formulas can be written in terms of the ratios of the frequencies.

A bat chirps for echolocation at 25 kHz. How fast would it have to be flying for you to hear it, at the upper threshold of human hearing, 20 kHz?

A singer sings a high note at 880 Hz. An interested bat comes flying in at 35 m/s. What frequency does the bat hear?
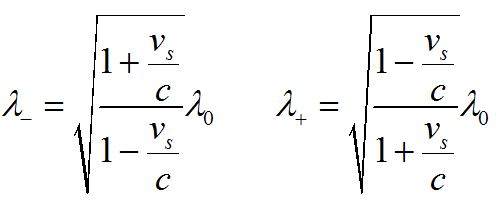

Courtesy of Astronomy Interactives: highered.mheducation.com/sites/0072482621/student_view0/interactives.html