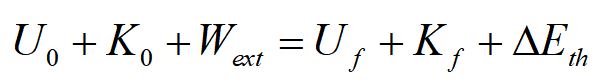Potential energy
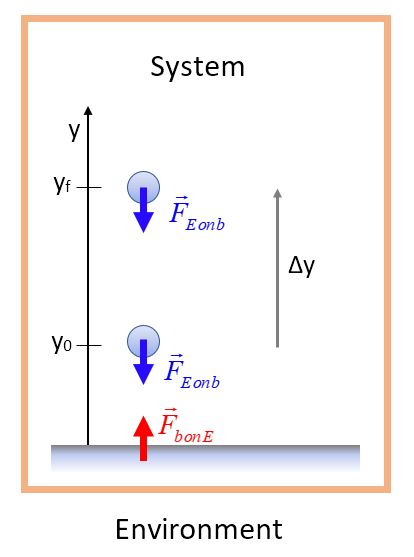
Potential energy is defined as the energy of interaction of objects within a system. We think of it as energy stored in the system. In the case illustrated here, a ball is thrown upward from the ground. We define our system as the ball + Earth, and the interaction involves the gravitational force between the ball and Earth.
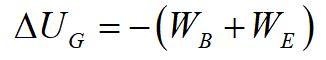
We can define the change in gravitational potential energy as the negative of the total work internal to the system, in this case, the sum of WB (the work done by gravity on the ball) and WE (the work done by gravity on the Earth). Since the displacement of the Earth is negligible, we typically can neglect the work done on the Earth.
It is important to note that potential energy involves position but not velocity.

Recall that work is defined as the dot product of force and displacement (for a constant force). Here, that means we can write the work done on the ball as the product of the gravitational force and its change in position in y.
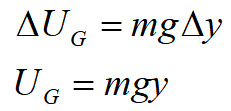
Recognizing that gravitational potential is the negative of the internal work allows us to write it in the form shown above. We are free to choose the zero of potential energy, and also where we have defined the position to be zero, so we typically choose the simpler form.
Elastic potential energy


In general, force is the gradient of a scalar potential energy.
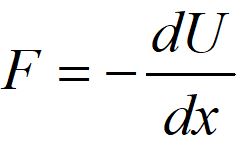
For a one-dimensional case, the relationship takes a simpler form.
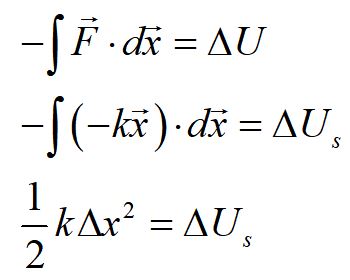
We can calculate the potential from a force by taking the negative integral of the force over a displacement.
For example, we can calculate the spring potential energy from the spring force. We find that spring potential energy of a mass on a spring is proportional to the square of the distance from equilibrium.
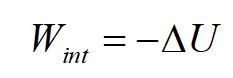
In general, the work done internally in a system equals the negative of the change of potential energy of the system.
Conservative and nonconservative forces
Conservative forces are forces that are path-independent and conserve mechanical energy. Non-conservative forces are path-dependent and dissipate energy.
Practice problems
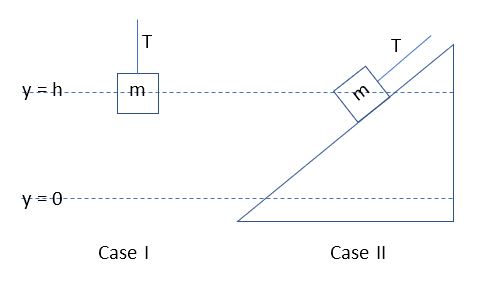
1. Work done by tension against gravity is done in two cases depicted below. In case A, a block of mass m is lifted to a height h. In case B, the block is pulled up a frictionless incline to the same height h. Compare work done against gravity on the block by the rope in the two cases.
A. WI < WII
B. WI = WII
C. WI > WII
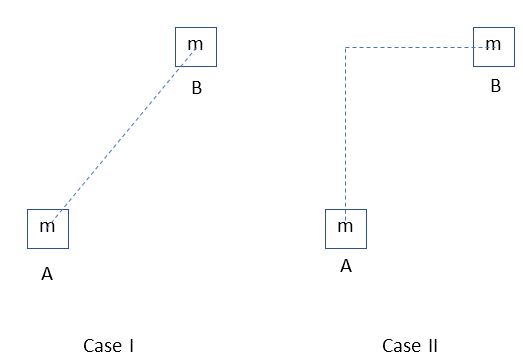
2. The diagram below shows a top-down view of a block of mass m that is pulled by a rope from position A to position B by two different paths. Assume there is friction between the block and the floor. Compare work done on the block by the rope against friction in the two cases.
A. WI < WII
B. WI = WII
C. WI > WII
Conservation of energy
As we noted earlier, neglecting energy of fusion and fission etc, energy cannot be created or destroyed, but can change form. Our full conservation energy equation is a mathematical statement of this fact.