Work

Work is energy that is transferred when an object is displaced by a force.

The stronger the force and the farther the displacement, the more work is done. Since force and displacement are vectors, it also matters how much they are aligned.

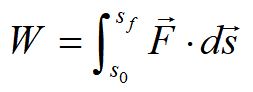
We define work as the force integrated over a displacement.

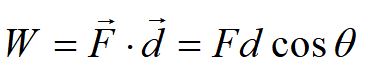
If the force is constant over the displacement, we can simply write work as force dotted with the displacement. Theta is defined as the angle between the force and displacement. Notice work is a scalar quantity, as we would expect, since it is transferred energy.

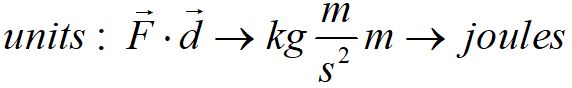
The units of work are Newton-meters, equivalent to joules.

As shown here, the work done by the applied force pulling the crate only includes the component of the force along the displacement of the crate.

Practice problems:

1. How much work is done by dragging a 2.5 kg crate with a tension force of 12 Newtons at angle 32⁰ for a distance of 5.0 meters?

2. How high could you lift the crate, doing the same amount of work?

Transfer of energy

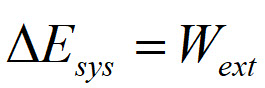
When a process transfers energy into or out of a system by mechanical means, we say that work was done on or by the system. The change in energy of the system equals the external work done.

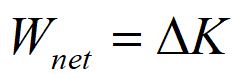
The total work done by all of the forces on an object equal the change in kinetic energy of the object. This is known as the work-kinetic energy theorem.

Work can be positive or negative. If a force is applied in a direction opposing the displacement, the work is negative.

Practice problems:

1. A dog pulls a 22 kg sled across frictionless snow. The tension in the cable is 1.5 N, at an angle of 12 degrees above the horizontal. What is the change in kinetic energy of the sled when the dog has pulled it 3.5 m?

2. Now assume we unhitch the dog, and there is friction between the sled and the snow. How much work has been done by friction if the initial speed of the sled is 1.2 m/s and it stops in 3.5 m?

3. An elevator of mass m starts from rest and accelerates upward with an acceleration a for a distance h. (use 9.8 m/s2 for g)

Assume:

   m = 1500 kg

    a = 1.2 m/s2

    h = 2.4 m

   A. How much work is done on the elevator by the gravitational force?

   B. How much work does the tension in the cable do on the elevator?

   C. How fast is the elevator moving when it reaches the height h?

4. An asteroid falls toward the moon. The force due to gravity takes the form:

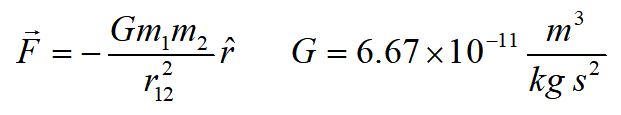
where m1 is the mass of the moon, m2 is the mass of the asteroid, r12 is the distance between them, and G is the gravitational constant. Assume the asteroid is moving directly toward the moon. What is the work done by gravity as the asteroid moves from r1 to r2?

The moon's mass is 7.3 x 1022 kg and the asteroid's mass is 2.1 x 1020 kg. Use r1 = 55,000 m and r2 = 28,000 m.