Free body diagrams

A free body diagram is a pictorial way to represent the forces acting on an object. It should include one object with all force vectors acting on it with relatively correct lengths as well as coordinate axes and any angles.

One of the most important thing to understand when drawing free-body diagrams is knowing what things are forces acting on an object and what things are not forces.

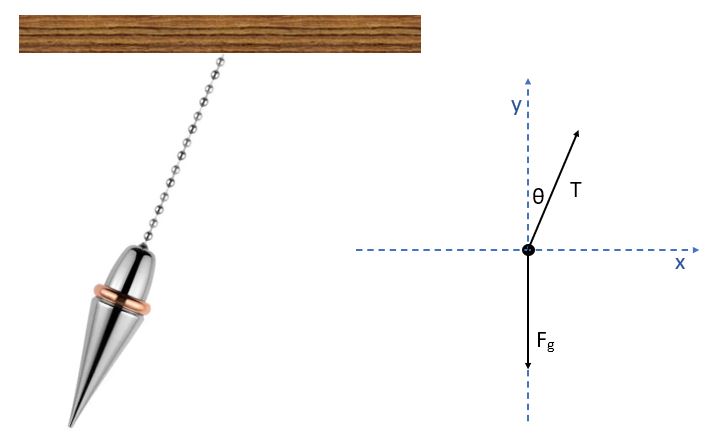
For the pendulum bob pictured above, what are the forces acting on it as it swings up through the air?

It might help to imagine what it feels like to be a pendulum bob swinging up through the air.

Also, remember that force is a vector. In general, acceleration is defined as a change in velocity. This means there is a force present when the direction of velocity changes, even though the speed may not change.

If an object is treated as a particle, we typically represent it as a dot. The force vectors are represented as arrows extending from the dot in the directions of the forces. The relative lengths of the arrows represent the relative magnitudes of the forces.

Here, the two forces acting on the ball are the force due to gravity in the downward direction and the normal force from the bat. The gravitational force is a non-contact force and the normal force is a contact force.

Normal force

In this case, the word "normal" is used to mean perpendicular. A normal force is a contact force that is perpendicular to a surface. In a sense, it arises to the magnitude that it "needs" to be. For example, the ground is exerting a larger normal force on the large dog in the photo above than it is exerting on the small dog. In each case, the normal force from the ground on the dog is equal and opposite to the normal force exerted on the ground by the dog.

Fundamentally, the normal force is the electromagnetic force, the repulsion felt by electrons between the two objects.

Consider a book sitting on a table. Consider the forces acting on the book and draw a free-body diagram of the book. Label any Newton's third law force pairs.

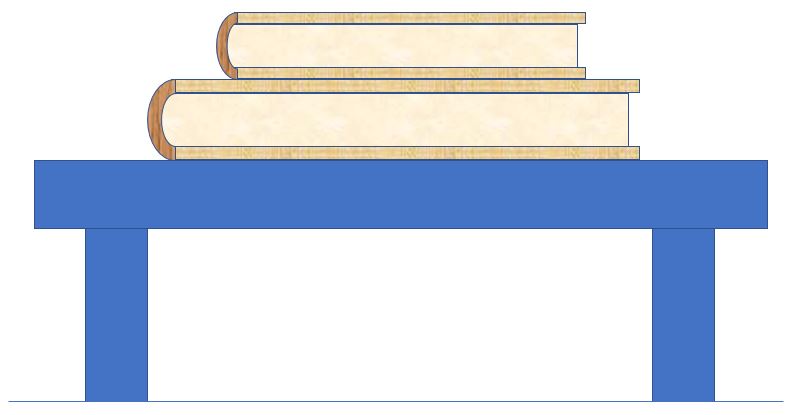
Now consider a system of two books stacked on a table, where the top book has less mass than the bottom book. Draw free-body diagrams of both books, keeping vector lengths consistent between the diagrams. Label any Newton's third law force pairs.

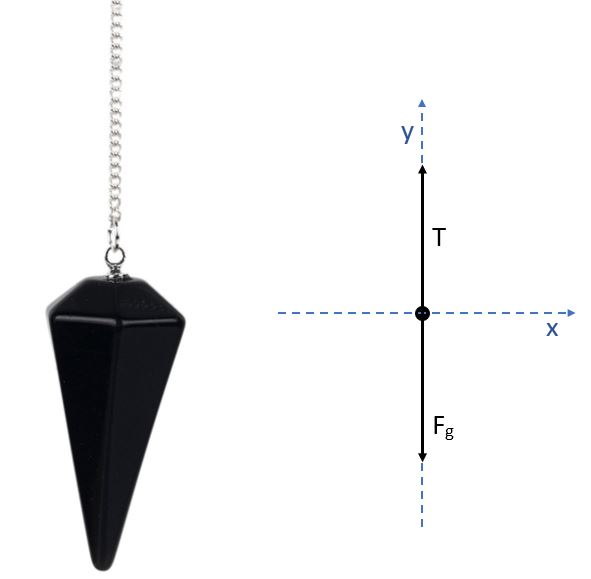
Here we have an object hanging from a chain. When we draw the free-body diagram, we indicate the force due to gravity in the downward direction and the contact force from the chain in the upward direction. The upward force is called a tension force, and it is transmitted along the chain. You can think of it as many contact forces as each link of the chain connects to the next.

Notice that the tension force is equal and opposite to the gravitational force, since the object is not accelerating. Be careful to note that even though the forces are equal and opposite, they are not a Newton's third law force pair. They cannot be, since they are acting on the same object. For example, the Newton's third law force pair of the gravitational force acting on the pendant from Earth would be the gravitational force on the Earth from the pendant.

An object can have more than one tension force acting on it, as shown here. Since the object is not accelerating, the net force on the object in both the x and y directions must each equal zero. The x-components of the tension forces cancel. The y-components of the tension forces must add together to be equal and opposite of the y-component of the gravitational force.

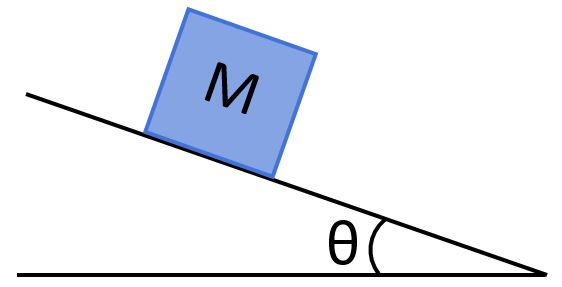
Consider a block of mass M that is at rest on a ramp. Draw a free-body diagram of the block.