Connected systems

Newton's third law states that forces come in pairs. The force of one object on a second equals the negative of the force of the second object on the first.

We write this NAB = -NBA. For the image above, the force that the parent uses to hold the child has the same magnitude of the force that the child exerts on the parent, and the two forces have opposite direction.

This simple law gives us a powerful tool for analyzing systems of multiple objects exerting forces. A tension can be thought of as many Newton's third law force pairs transmitting the force along the cord. If the cord is massless and inelastic, the forces will have equal magnitudes at the ends of the cord.

Sample problems:

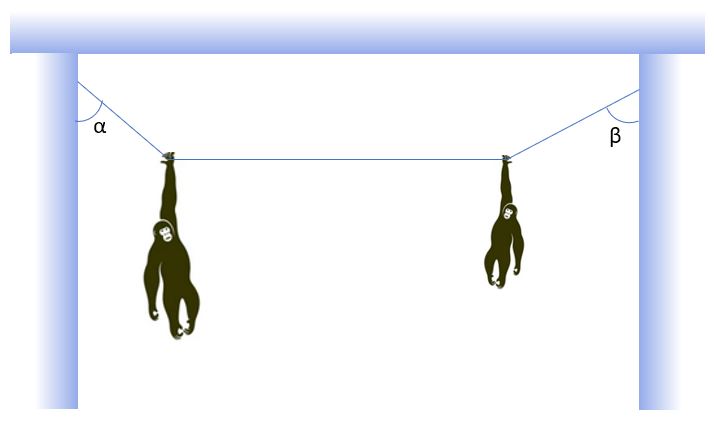
2. Viona and her young orangutan Nim are hanging at rest on a cord. Assume that the cord is horizontal between them. We measure the angle α to be 32° and we know Viona weighs three times as much as Nim. What is the angle β? What is the tension in the cord between Nim and the wall?

Pulleys

An ideal pulley is assumed to be massless and frictionless. A single pulley redirects a cord, changing the direction of the force but not its magnitude. A more complicated system can be analyzed using free-body diagrams and force equations for each massive object in the system.

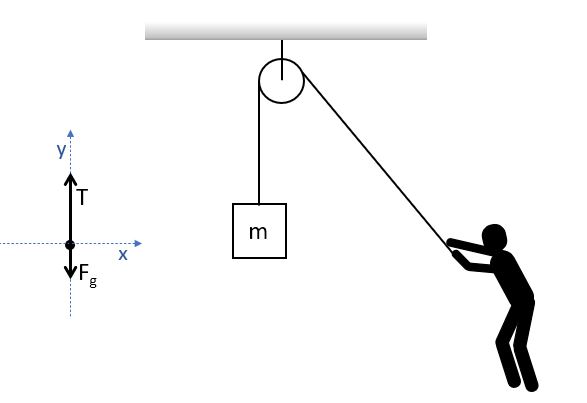
For example, let's analyze a massive block being accelerated upward by a person pulling a rope over a pulley as shown. Notice that the free-body diagram indicates that the tension has larger magnitude than the gravitational force, so that the net force would be upward.

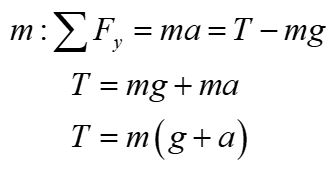
Using the free-body diagram as a guide, we derive the net force equations for this system. We find that the tension is the mass of the block times the sum of the acceleration of the block and the gravitational acceleration.

Attaching a second pulley to the block changes the system considerably. Note that there are two tension forces on the block now, one for each segment of rope connecting to the block + pulley. For this problem, we want to keep the acceleration the same as the first case, so the tensions are half as strong.

Practice problems:

1. Find the tension in the rope for the case pictured above, using the same acceleration and mass of the block. Assume the pulleys are ideal, that is, they  are frictionless and massless.

2. Compare the length of rope pulled for the two cases, assuming the block was raised the same distance in both cases.

More practice problems

1. An object of mass m hangs on a massless cord over a massless, frictionless pulley. The cord is attached to the wall as shown. What is the tension in the cord? Assume the object has mass 3.2 kg, use g = 9.8 m/s2.

2. An object of mass m hangs on a massless cord over a massless, frictionless pulley. The cord is attached to a block of mass M on a frictionless table. What is the tension in the cord? Assume the object has mass 3.2 kg and the block has mass 4.6 kg; use g = 9.8 m/s2.

5. A person of mass M pulls himself upward using a frictionless massless pulley apparatus as shown. Find the pulling force Fpull that he needs to pull on the rope to accelerate himself upward. Consider the case where his acceleration is 0.20 m/s2 and his mass (including the chair) is 80 kg.

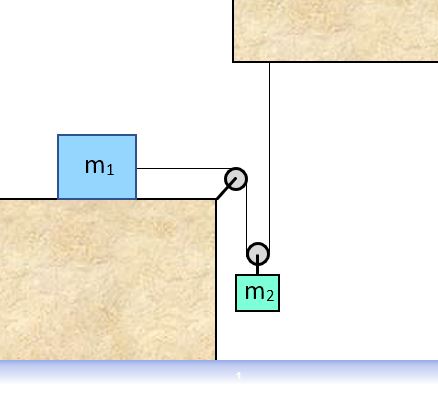
6. Blocks of mass m1 = 2.6 kg and m2 = 1.4 kg are attached as shown by a massless inelastic cord over identical massless frictionless pulleys. Block m1 is released from rest and allowed to accelerate.

Find the acceleration of block m2.

9. Consider a block of mass M on a frictionless table connected by massless inelastic cords over identical frictionless massless pulleys to hanging blocks of mass m1 and m2 where m2 > m1.

Find the acceleration of the system.

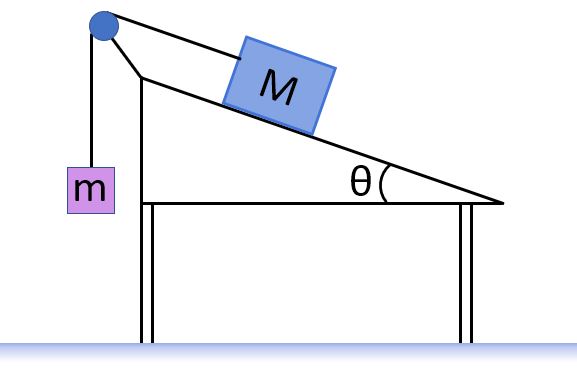
10. Consider a block of mass M on a ramp of angle θ. The block is attached by massless strings over identical massless, frictionless pulleys to two hanging blocks of mass m1 and m2. Assume that the block of mass M is accelerating down the ramp and that there is no friction between it and the ramp.

What is the magnitude of the tension in the string attached to m2?