Rigid rotational motion
- Center of mass
- Rotational energy
- Moment of inertia
- Torque
-
Rotational dynamics
- Fixed axis
- Static equilibrium
- Rolling
- Vector description
- Angular momentum conservation
Center of mass
The center of mass of an object or a system of objects is a weighted sum, defined as the sum of the produce of mass and position weighted by the total mass.
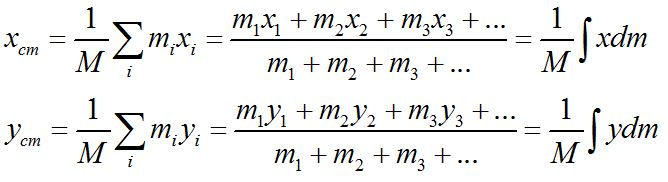


The center of mass of an object does not necessarily lie within the object, as is obvious with this boomerang. An unconstrained object rotates about its center of mass.
© 2005 Pearson Prentice Hall, Inc
2. A broom balances at its center of mass. If you saw the broom through its center of mass and weigh the two parts, which part will weigh more?
Moment of inertia
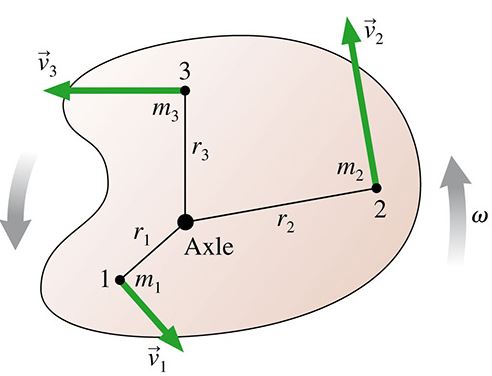
A rotating object has kinetic energy due to the motion of its particles.
© 2013 Pearson Education, Inc
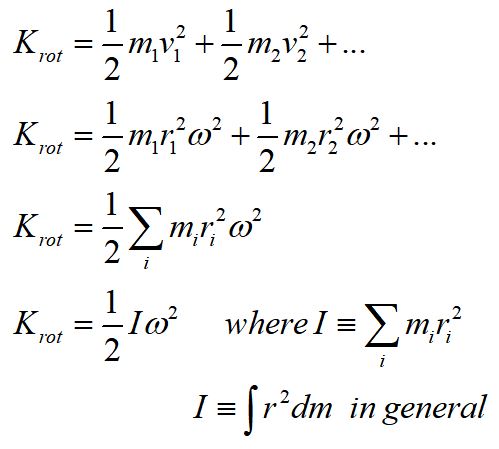
Note that the radius for each mass element is the distance of the mass element from the axis of rotation.
The moment of inertia, I, is a measure of the mass distribution of a rotating object. Its definition depends on the axis of rotation. A larger moment of inertia means an object needs more torque to produce an angular acceleration.
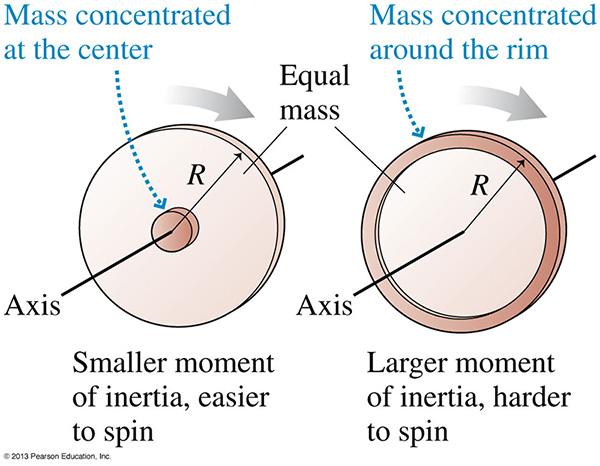
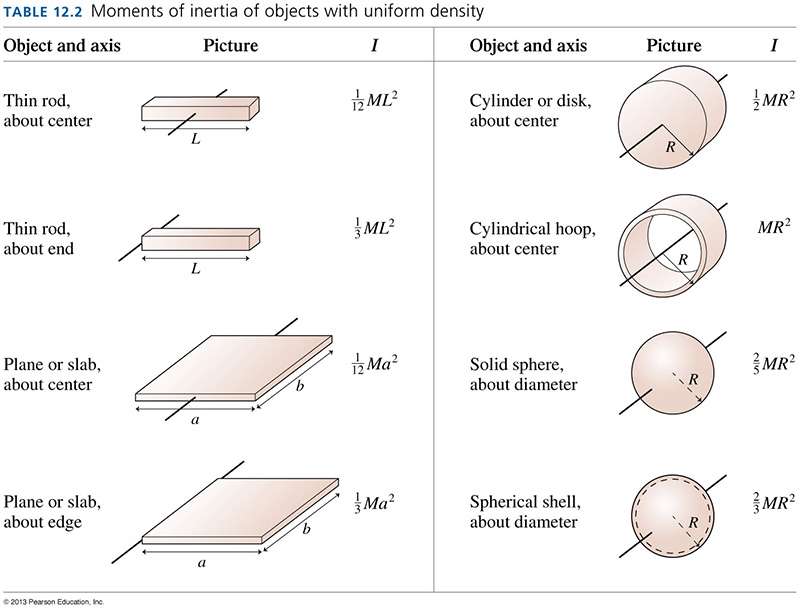
3. Consider a ball and a solid cylinder, both with constant mass density. Assume they have the same mass and the same radius. They both start from rest and start to roll down a ramp at the same time. Which reaches the bottom first?

4. Using the concept of the moment of inertia, which do you think would be easier to balance, a hammer with head up or a hammer with head down?
A. head up
B. head down
C. they would be the same
5. A rod of mass m and length L is hinged to a wall as shown and released from rest, allowing it to rotate downward. What is the speed of the tip of the rod when it hits the wall?

Parallel axis theorem
If an object is made to rotate about an axis that does not go through the center of mass, the moment of inertia can be found using the parallel axis theorem.
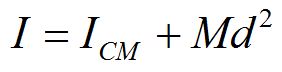
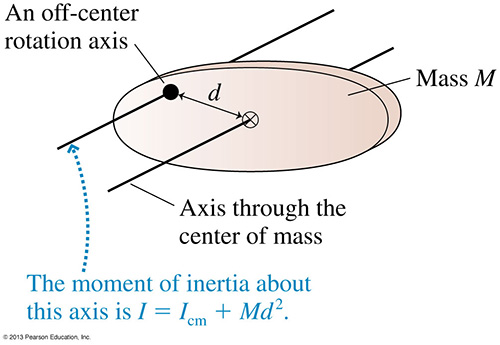
Image source