Angular momentum

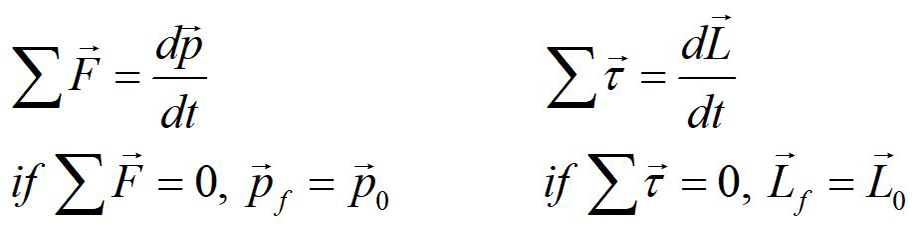
In the absence of net external forces, linear momentum is conserved.

In the absence of net external torques, angular momentum is conserved.

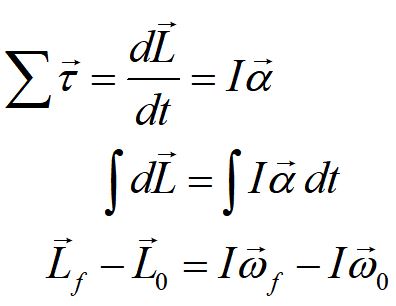
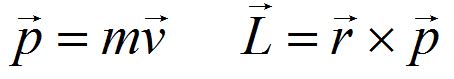
Angular momentum can take two forms. For a rotating object, angular momentum is equal to the product of the moment of inertia and the angular velocity. For a point particle, the moment of inertial is the cross product of the particle's position and momentum.

A skater spins up when she brings her arms in toward her rotation axis, reducing her moment of inertia. To conserve angular momentum, her angular speed must increase.

Sample problems

1. Two buckets spin around in a horizontal circle on frictionless bearings. Suddenly, it starts to rain. What happens? Do the buckets speed up, slow down or continue rotating at the same angular speed?

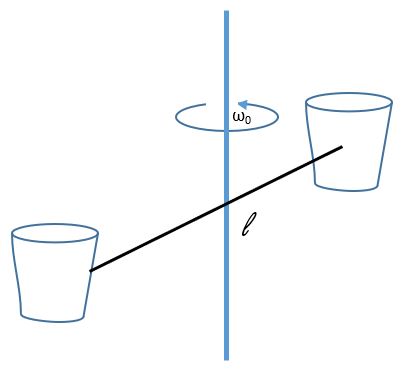
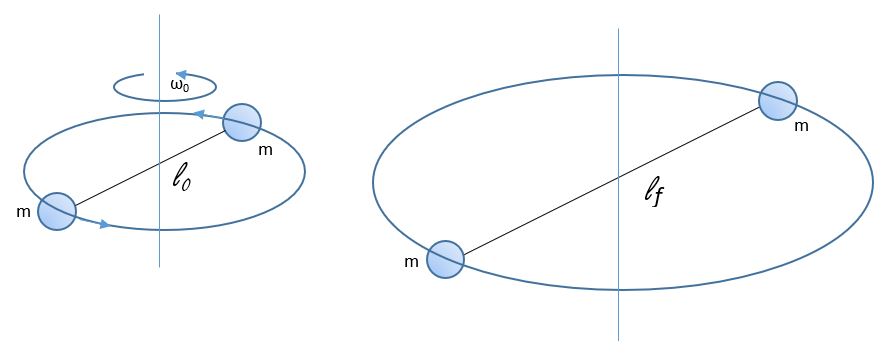
2. For a system consisting of two masses connected by a massless rod, angular momentum is conserved when the rod expands to twice its original length. Find the final angular velocity of this system, in terms of its initial angular velocity.

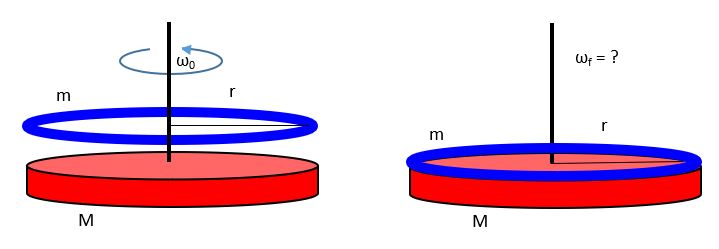
4. A uniform solid cylinder with mass M and radius r is initially at rest. A projectile with mass m and speed v approaches as shown and sticks to the outer edge of the cylinder. Assume that there is no final translational motion of the system.

Find the final angular speed of the system.

Rotational motion:

4 approaches to problem solving

Putting it all together

There are four main approaches to solving problems for systems involving rotation:

1. Forces and torques
2. Conservation of energy
3. Conservation of angular momentum
4. Rotational kinematics

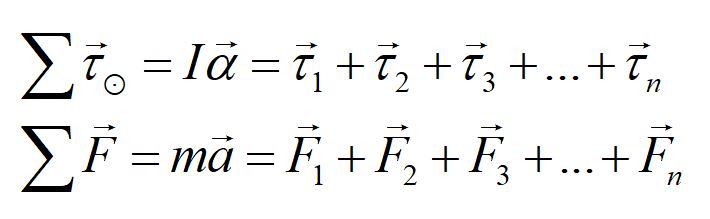
Using a net force and net torque approach involves solving vector equations. Note that the torque equation is taken about a pivot point. These fundamental equations provide a system of equations to be solved simultaneously.

For cases of static equilibrium, the net torque and the net force each equal zero. For dynamic cases, you may need to include kinematic equations.

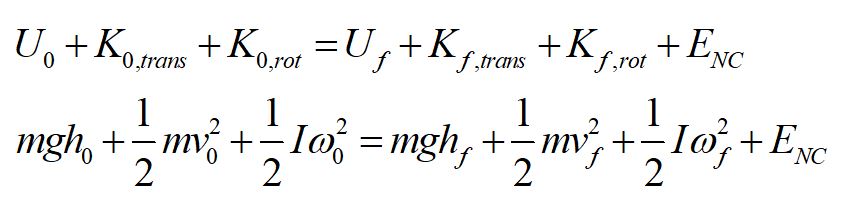
Conservation of energy includes rotational energy as well as translational energy. Non-conservative energy such as energy lost to friction is included in the final state.

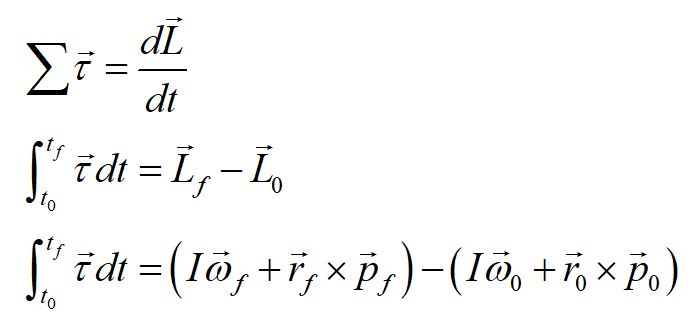
A conservation of angular momentum approach may be used for systems involving rotation. A system may include rotating objects with moment of inertia I and translating objects of momentum p, each having and initial and final angular momentum.

Kinematic equations for constant linear and rotational acceleration are shown here. For more general equations, refer to the previous chapter.

Often, a problem can be solved in multiple ways, or with a combination of approaches. Taking advantage of symmetries in the system may make one approach easier than another. Also, be careful to recognize the external forces or torques in a problem when deciding which approach to take.